You have not paid for this chapter
Algebra
Chapter 23
Problem 2
Select a different problem
Example:
Find the roots of:
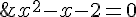
Since the equation has x to the power two, (x
2) there are two roots. The equations for the roots are:
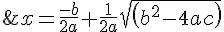} )
and
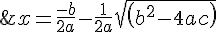} )
The a, b, and c coefficients are found from the general form of the equation:
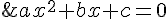
Thus, for this example, a = 1, b = -1, and c = -2. Substituting these into the two roots you get
First Root:
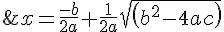}=\frac{1}{2}+\frac{1}{2}sqrt(1+8)=\frac{1}{2}+\frac{3}{2}=2 )
Second Root:
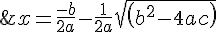}=\frac{1}{2}-\frac{1}{2}sqrt(1+8)=\frac{1}{2}-\frac{3}{2}=-1 )
So the two roots are x = 2, and x = -1. If you substitute these back into the original equation, you get:
First Root (2):
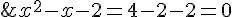
which is true, and
Second Root (-1):
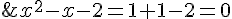
which is also true
Thus, you prove the two roots (2 and -1) are the two roots of the equation.
Another way to check if the roots are correct is to plot the equation on the graph below.
The way to do this is to type x^2 - x - 2 in the box to the right of Function f(x).
Then click on the Plot Graph button. The function will then be plotted on the graph.
The positions where the graph crosses the x-axis are x = 2 and x = -1.
These are the solutions (roots) of the equation.